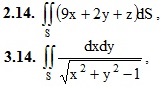- Arts & Culture 5939
- Business & Economics 689
- Computers 319
- Dictionaries & Encyclopedias 81
- Education & Science 75882
- Abstracts 252
- Astrology 4
- Astronomy 1
- Biology 8
- Chemistry 2221
- Coursework 15546
- Culture 9
- Diplomas 411
- Drawings 574
- Ecology 6
- Economy 83
- English 75
- Ethics, Aesthetics 3
- For Education Students 17613
- Foreign Languages 11
- Geography 3
- Geology 1
- History 89
- Maps & Atlases 5
- Mathematics 13856
- Musical Literature 2
- Pedagogics 19
- Philosophy 23
- Physics 14857
- Political Science 5
- Practical Work 101
- Psychology 60
- Religion 4
- Russian and culture of speech 8
- School Textbooks 7
- Sexology 42
- Sociology 9
- Summaries, Cribs 87
- Test Answers 150
- Tests 9243
- Textbooks for Colleges and Universities 32
- Theses 24
- To Help Graduate Students 14
- To Help the Entrant 37
- Vetting 364
- Works 13
- Информатика 10
- Engineering 3063
- Fiction 696
- House, Family & Entertainment 107
- Law 132
- Website Promotion 71
DHS 15.1 - Option 14. Decisions Ryabushko AP
Refunds: 0
Uploaded: 17.01.2024
Content: 14v-IDZ15.1.doc 168 kB
Product description
1. Dana function u (M) = u (x, y, z) and the point M1, M2. Calculate: 1) The derivative of this function in the direction of the point M1 M1M2 vector; 2) grad u (M1)
1.14. u (M) = ln (1 + x + y2 + z2), M1 (1, 1, 1), M2 (3, -5, 1)
2. Calculate the surface integral of the first kind on the surface S, where S - part of the plane (p), cut off by the coordinate planes.
(P): 2x + y + z = 4
3. Calculate the surface integral of the second kind.
where S - the surface of the hyperboloid x2 + y2 = z2 + 1 (the normal vector n which forms an obtuse angle with the unit vector k), cut off by the plane z = 0 and z = √3.
4. Calculate the flow vector field a (M) through the outer surface of the pyramid formed by plane (p) and the coordinate planes in two ways: a) determination using flow; b) using the formula Ostrogradskii - Gauss.
4.14. and (M) = 4xi + (x - y - z) j + (3y + 2z) k, (p): 2x + y + z = 4
Additional information
Detailed solution. Decorated in Microsoft Word 2003 (Quest decided to use the formula editor)
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
Feedback
0| Period | |||
| 1 month | 3 months | 12 months | |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |